Return to Statement

Radius, Between Two Surfaces Example

Creating a cylinder tangent to two previously defined sheets. The cylinder is bounded by two planes (PL(1) and PL(2)). PT(1) determines the quadrant in which the cylinder is constructed. PT(2) determines which portion of the cylinder is to be created. In the case below, the limiting planes are parallel and the cylinder would be created on only one side. However, the second point is still required.

$$

$$  Declarations

$$

    ENTITY/PT1,PT2,SURF(2),PL(2),CYL1

$$

$$ Geometry Definition

$$

    PT1 = POINT/0,0,0

    PT2 = POINT/-1,-1,0

    SURF(1)= PLANE/XYPLAN,1

    SURF(2)= PLANE/XZPLAN,-1

    PL(1) = PLANE/YZPLAN,0

    PL(2) = PLANE/YZPLAN,-2

$$

$$ Cylinder Definition
 
$$

    CYL1 = CYLNDR/SURF(1),SURF(2),CENTER,PT1, $ RADIUS,1,PL(1),PL(2),PT2

  

   

  

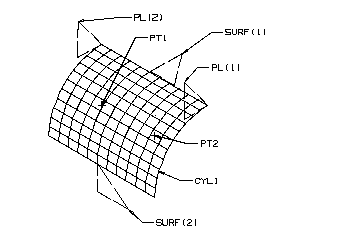
   Fillet Cylinder Bounded by Two Parallel Bounding Planes

  

Example
  

   Creating a cylinder tangent to two previously defined sheets. The 
   cylinder is bounded by two planes (PL(1) and PL(2)). In this case the 
   planes intersect causing the possibility of two cylinder halves to be 
   created. The half closest to PT2 is created.
$$
$$  Declarations
$$
    ENTITY/PT1,PT2,SURF(2),P(6),PL(2),CYL1
$$
$$ Geometry Definition
$$
    PT1 =POINT/0,1,-1
    PT2=POINT/0,-1,0
    SURF(1)=PLANE/XYPLAN,0
    SURF(2)=PLANE/XZPLAN,0
    P(1) =POINT/0,0,0
    P(2)=POINT/0,1,0
    P(3)=POINT/1,0,1
    P(4)=POINT/-.5,0,0
    P(5)=POINT/-.5,1,0
    P(6)=POINT/-1,0,1
    PL(1)=PLANE/P(1..3)
    PL(2)=PLANE/P(4..6)
    BLANK/P(1..6)
$$
$$ Cylinder Definition
$$
    CYL1=CYLNDR/SURF(1),SURF(2),CENTER,PT1,$
    RADIUS,1,PL(1),PL(2),PT2


  

   
  

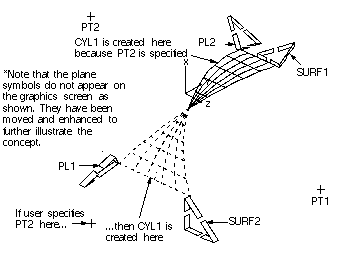
   Fillet Cylinder Bounded by Two Non-parallel Planes
  

   In the figure shown above, the upper cylinder half is created because 
   of its proximity to PT2. If PT2 had been specified in -Z, the 
   lower cylinder half would have been created.