样条曲线

Synopsis

obj = SPLINE/[CLOSED,]{point[,{VECT,dx,dy,dz|TANTO,curve|angle}]}+

Description

Spline allows you to create a spline through a series of previously defined points. The resulting spline is generated by cubic (third order) polynomials. The optional minor word CLOSED causes the first point to be automatically assumed as the last point and the spline to be closed. In a closed spline, the starting slope is forced to be equal to the slope at the ending point. If the CLOSED minor word is omitted, the spline is open even if the first and last points are coincident and the starting and ending slopes are not forced to be the same.

A maximum of 102 arguments may be stated in the spline definition. If each knot point, for example, has an associated vector, tangency point, or angle, only 51 knot points could be used in the statement. Subranges can be used to exceed this limitation.

The format below shows the series of options (except the minor word CLOSED) which are repeated for each point in the spline. At least two points must be specified.

Using the Approximate Curves method creates a spline which approximates a list of previously defined objects. The spline can be created to a tolerance, or by approximating each spline segment for each object in the list.

Parameters

Parameter

Description

CLOSED

Minor word that indicates that the spline is closed on itself whether or not the first and last points are coincidental. The beginning and ending of the spline is also tangent at the first point.

point

An object list or array which represents a series of previously defined points that the spline passes through.

NOTE: The following parameters represent various ways of controlling the slope of the spline at each point in the object list/array. Several slopes can be specified and are matched with points in order beginning with the first point in the object list.

You can repeat point and tangent specifications as many times as needed in a single statement (up to 102 arguments). You can specify more points than tangents parameters.

VECT

Minor word that indicates that the slope of the spline at the previous point is to be defined as a Vector by the values in the next three fields.

dx,dy,dz

Three work coordinate values which represent the components of the slope vector.

TANTO

Minor word that indicates that the slope of the spline at the previous point is to be defined as being tangent to a specified curve.

curve

A previously defined object which is used to define the slope of the spline.

angle

Numerical value which defines the slope of the spline at the previous point in degrees measured counterclockwise from the positive X Axis.

NOTE: Definition of the slope of the spline can be performed in any one of the three mutually exclusive manners above. You may mix the methods in any SPLINE statement as long as you use only one method for any one point.

Example

Creating a spline with no slope controls specified. In this case, the spline is fit through the points as smoothly as possible. An open and closed splines are created with the same points.

Declarations

ENTITY/P(4),SPLN(2)

Geometry Definition

P(1)=POINT/-1,0
P(2)=POINT/0,0
P(3)=POINT/1,.866
P(4)=POINT/2,.75

Spline Definition

SPLN(1)=SPLINE/P
SPLN(2)=SPLINE/CLOSED,P

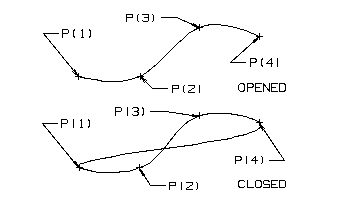
An Open and Closed Spline through the Same Points

Example

Creating a spline with no slope controls specified. In this case, the spline is fit through the points as smoothly as possible. Open and closed splines are created with the same points.

Declarations

ENTITY/P(4),SPLN(2)

Geometry Definition

P(1)=POINT/0,0
P(2)=POINT/1,-1
P(3)=POINT/2,0
P(4)=POINT/1,1

Spline Definition

SPLN(1)=SPLINE/P,P(1)
SPLN(2)=SPLINE/CLOSED,P

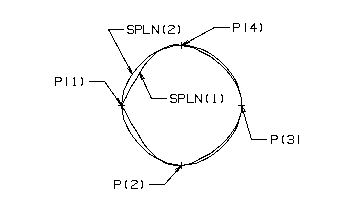
A Closed and Open Spline Where the End Points Are Coincident

Example

Creating a spline using the minor word VECT followed by the three component values of the desired vector. The spline, at this point, is tangent to the specified vector.

Declarations

ENTITY/P(5),SPLN1

Geometry Definition

P(1) =POINT/-1,0
P(2)=POINT/0,0
P(3)=POINT/1,.866
P(4)=POINT/2,.75
P(5) =POINT/3,1.5

Spline Definition

SPLN1=SPLINE/P(1),P(2),VECT,1,2,0,P(3),P(4),$
VECT,-1,-2,0,P(5)

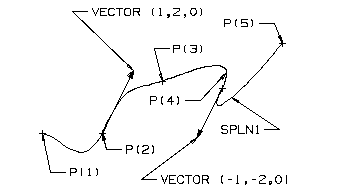
A Spline Constrained by Vectors

Example

Creating a spline using the minor word TANTO and an existing curve. The curve tangent of the spline, at this point, is parallel to the curve tangent of the specified curve at its closest end point.

Declarations

ENTITY/CR(3),P(3),SPLN1

Geometry Definition

CR(1)=CIRCLE/-2,0,.5,START,270,END,330 CR(2)=CIRCLE/0,1,.5,START,180,END,270 CR(3)=CIRCLE/1.5,0,.5,START,180,END,270
P(1)=POINT/-1,-1
P(2)=POINT/0,0
P(3) =POINT/1,-1

Spline Definition

SPLN1=SPLINE/P(1),TANTO,CR(1),P(2),TANTO,CR(2),$
P(3),TANTO,CR(3)

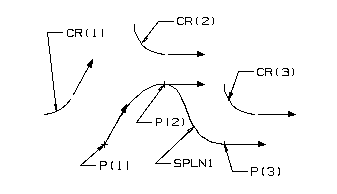
A Spline Constrained by Curves and Vectors

Example

Creating a spline by specifying an angle at which the spline is to be tangent. The angle is measured with respect to the X axis of the work coordinate system.

Declarations

ENTITY/P(4),SPLN1

Geometry Definition

P(1)=POINT/-1,0
P(2)=POINT/0,0
P(3)=POINT/1,.866
P(4)=POINT/2,.75

Spline Definition

SPLN1=SPLINE/P(1),90,P(2),300,P(3),90,P(4),300

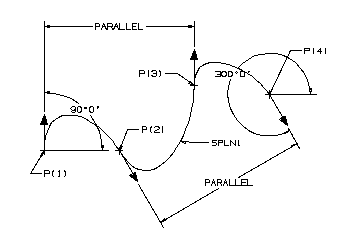
A Spline Constrained by Angles

Example

Demonstrates the use of subrange operators to exceed the knot point limitations in the SPLINE command. This example demonstrates that the statement

SPLINE/P(1..9),VECT,V(1..6),P(10..11),A(5..6)

is equivalent to

SPLINE/P(1),VECT,V(1),V(2),V(3), $
P(2),VECT,V(4),V(5),V(6), $
P(3),P(4),P(5),P(6),P(7),P(8),P(9), $
P(10),A(5),P(11),A(6)

The following statement found at the end of the program demonstrates how to avoid exceeding the maximum of 102 arguments.

SPL3=SPLINE/P(1..500),VECT, V(1..1500),P(501..1000),A(1..500)

Declarations

 
   ENTITY/P(1000),SPL1,SPL2,SPL3
   NUMBER/V(1500),A(500),I,J
   &ENTCLR = &RED
   J = 1
   DO/L1:,I,1,1000
   P(I) = POINT/I,J,-J
   IF/J==1,JUMP/ELSE1:
   J = 1
   JUMP/END1:
   ELSE1:
   J=-1
   END1:
   L1:
   DO/L2:,I,1,500
   V(I*3-2) = -1.0
   V(I*3-1) = 0.0
   V(I*3) = 0.0
   L2:
   DO/L3:,I,1,500
   A(I) = 180.0
   L3:
   SPL1 = SPLINE/P(1),VECT,V(1),V(2),V(3), $
           P(2),VECT,V(4),V(5),V(6), $
           P(3),P(4),P(5),P(6),P(7),P(8),P(9), $
           P(10),A(5),P(11),A(6)
   MESSG/'SPLINE #1'
   &ENTCLR = &CYAN
   SPL2 = SPLINE/P(1..9),V(1..6),P(10..11),A(5..6)
   MESSG/'COMPARE SPLINE #2'
   BLANK/SPL1,SPL2
   $$
   &ENTCLR = &YELLOW
   SPL3 = SPLINE/P(1..500),VECT, V(1..1500),P(501..1000),A(1..500)
   HALT

Parameter	Description
CLOSED	Minor word that indicates that the spline is closed on itself whether or not the first and last points are coincidental. The beginning and ending of the spline is also tangent at the first point.
point	An object list or array which represents a series of previously defined points that the spline passes through.

VECT	Minor word that indicates that the slope of the spline at the previous point is to be defined as a Vector by the values in the next three fields.
dx,dy,dz	Three work coordinate values which represent the components of the slope vector.
TANTO	Minor word that indicates that the slope of the spline at the previous point is to be defined as being tangent to a specified curve.
curve	A previously defined object which is used to define the slope of the spline.
angle	Numerical value which defines the slope of the spline at the previous point in degrees measured counterclockwise from the positive X Axis.