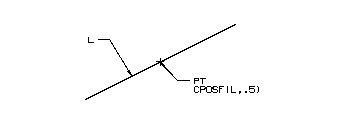
The following example shows the use of the CPOSF function.
ENTITY/L,PT
NUMBER/A(3)
|
Statement |
Assigned Value |
|
L=LINE/0,0,2,1 |
|
|
A=CPOSF(L,.5) |
A(1)=1,A(2)=.5,A(3)=0 |
|
PT=POINT/A |
|
The point PT is essentially the midpoint of the line.

Point PT is Created at the Midpoint of the Line L
If the scalar value is between 0 and 1, the returned coordinates lie on the curve. If the scalar is less than 0 or greater than 1, the returned coordinates lie on the extension of the curve. Determining where the position lies on the curve extension depends on the type of curve.
When using a line, the amount of extension is based on the length of the line. For example, a scalar value of 1.25 would return the coordinates of a point on the line extension 1/4 of the line length past the endpoint of the line. Similarly, a scalar value of -.25 would return the coordinates of a point on the line extension 1/4 of the line length before the start point of the line. Therefore, obtaining the desired coordinates is dependent on knowing the direction in which the line was constructed.
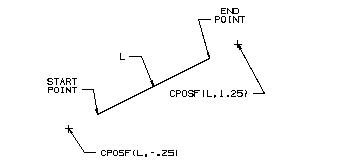
Points on the Extension of a Line
When using an arc or an ellipse, the amount of extension is based on the angular sweep of the object. For example, an arc which is defined from 10_ to 80_ has an angular sweep of 70_. Therefore, a scalar value of 1.5 would return the coordinates of a point on the extension 35_, 1/2 the total sweep angle, past the end of the arc. Since arcs and ellipses are constructed in a counterclockwise direction, a positive scalar value assumes an extension in the counterclockwise direction and a negative scalar value assumes an extension in the clockwise direction, with respect to the CSYS of the conic.
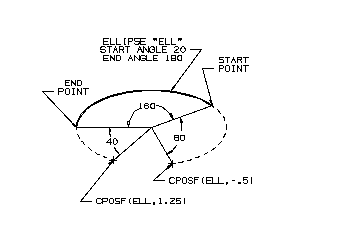
Points on the Extension of an Ellipse
When using a parabola or a hyperbola the amount of extension is based on the linear distance between the minimum and maximum "Y" value of the curve with respect to the CSYS of the conic. The maximum and minimum "Y" values limit the sweep of the curve on the positive and negative side of the axis of symmetry. Therefore, a positive scalar value assumes an extension on the maximum "Y" side of the axis of symmetry and a negative scalar value assumes an extension in the minimum "Y" side of the axis of symmetry.
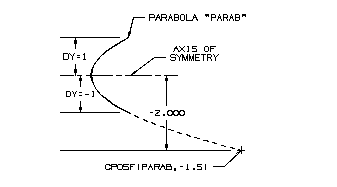
Points on the Extension of a Parabola
When using a spline, the amount of extension is based, to some degree, on the length of the spline. Unlike lines and arcs, however, the relationship between the length of the spline and the specified percentage does not always have a one to one correspondence. In addition, since the derivative vectors at the start and end of a spline affect the direction of the extensions, determining where the position on a curve extension lies may be only an approximation.
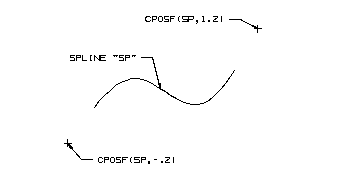
Points on the Extension of a Spline